Design Information Bulletin No. 60 (DIB #60)
Operational and Safety Improvements at Freeway Interchanges
The purpose of this DIB is to disseminate the results of research studies on methods of rehabilitating freeway interchanges that develop operational and safety problems after construction.
State of California Memorandum
Date: November 4, 1982
To: All District Directors
Attention Project Development Branch Chiefs and Fred Jackson, Chief, Sacramento Project Design Unit
From: Department Of Transportation, Division of Transportation Facilities Design, Office of Planning and Design
Subject: Design Information Bulletin 60 - Operational and Safety Improvements at Freeway Interchanges
Purpose:
To disseminate the results of research studies on methods of rehabilitating freeway interchanges that develop operational and safety problems after construction.
Distribution:
It is recommended that copies of this Bulletin be distributed down to the Project Design Engineer level.
Background:
A recent research report published by FHWA includes a systematic method of identifying alternatives for freeway interchange improvement projects. Information is presented in a series of 9 charts that relate the more common operational and safety problems of freeway-arterial interchanges to potential solutions.
The application of this procedure should help designers find the best solution without limiting the range of solutions or excluding the exercise of engineering judgment.
Recommendation For Use:
The attached charts and text are reprinted verbatim from report No. FHWA/RD-81/104,Volume II Design Procedures for Rehabilitation of Freeway-Arterial Interchanges, dated May 1982.
Use of the charts is discretionary not mandatory. They are intended as design aids in the preparation of PWP's and Project Reports for interchange rehabilitation projects.
A copy of the complete FHWA report has been sent to each District and the Headquarters Transportation Library.

DIB-60 Design Guidance and Standards

VI. Identify Improvement Alternatives
Once a problem interchange has been identified and the nature of the problem has been thoroughly investigated through engineering studies, the next step is to identify alternative solutions to alleviate the problem. A procedure for identifying improvement alternatives is presented below.
A. Procedure to Identify Alternatives
The selection of a set of suitable alternative solutions for a particular interchange problem is highly dependent on the type of operational or safety problem(s), the interchange configuration, the geometrics of individual interchange elements, the traffic volumes present, the type of traffic control devices used, the right-of-way, and other physical constraints and many other factors. Because so many factors are involved, it is often stated that the problems of each interchange are unique and require a unique solution; and, in the strictest sense, this is true. However, it is also true that certain general classes of problems recur frequently and that certain general classes of solutions are appropriate for these problems. Therefore, we have attempted to organize the state-of-the-art in a manner that will be useful to designers and traffic engineers who deal with freeway-arterial interchange problems.
Currently, engineers identify appropriate alternative solutions through engineering judgment based on previous experience with interchanges having operational and safety problems. Although a more formalized approach is recommended here, it is not our intention to supplant the engineer’s judgment. Rather, we hope to assist the engineer by making the review of potential solutions as efficient as possible. At the same time, we want to ensure that the range of alternative solutions is not limited unnecessarily. An organized procedure to review potential solutions should reduce the possibility that the “best” solution will be missed.
The recommended approach uses a series of nine charts (presented in Tables 4-12) that relate the common operational and safety problems of freeway-arterial interchanges to potential solutions. Each chart presents appropriate solutions for a specific problem or a set of related problems. Where several distinct problems are present at an interchange, the use of more than one chart may be required to identify all appropriate solutions. The potential solutions are classified by the type of ramp or interchange configuration to which they are appropriate, and by whether the overall interchange configuration or only a portion of interchange (freeway, ramp, or arterial crossroad) is to be modified.


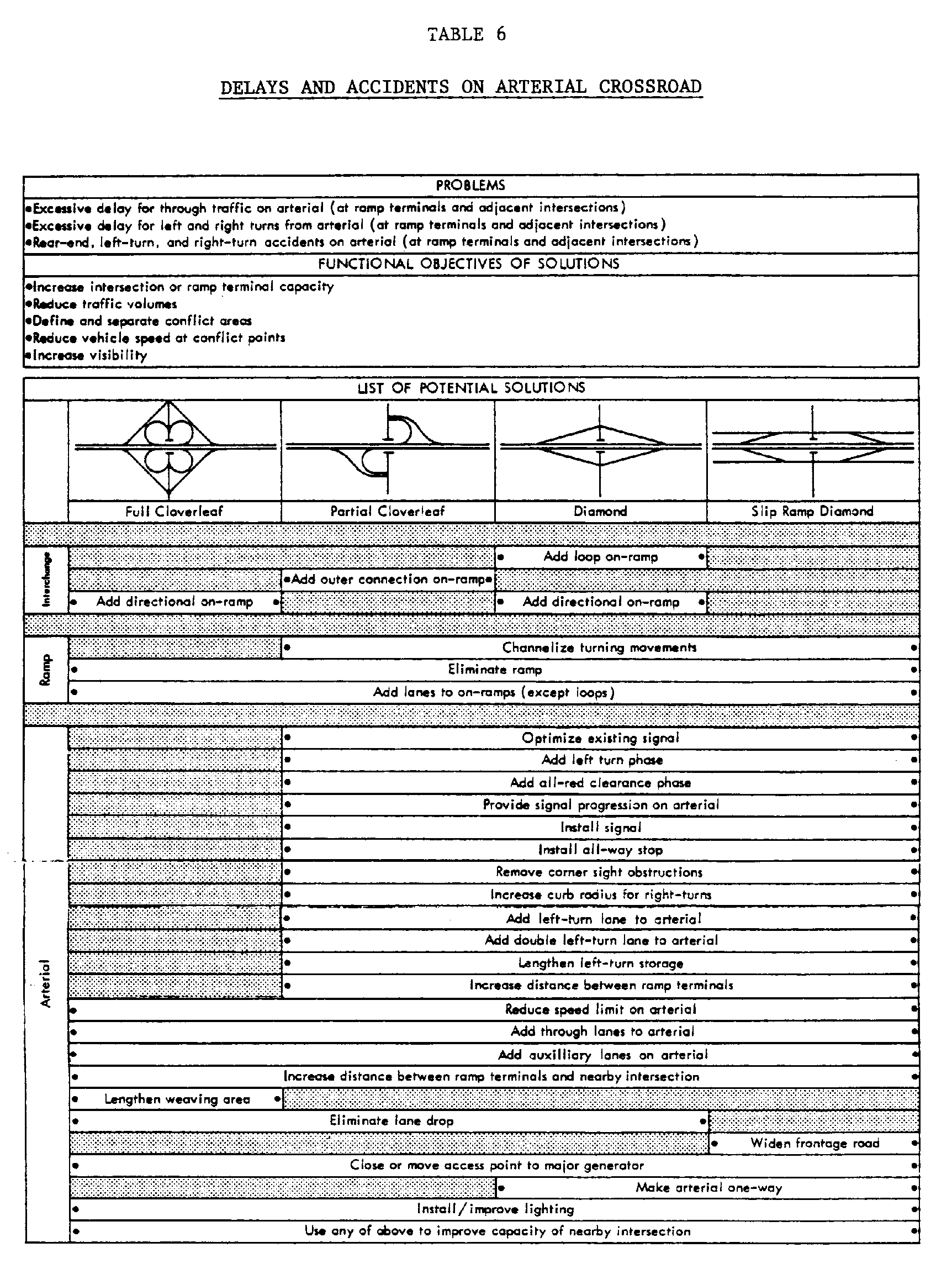
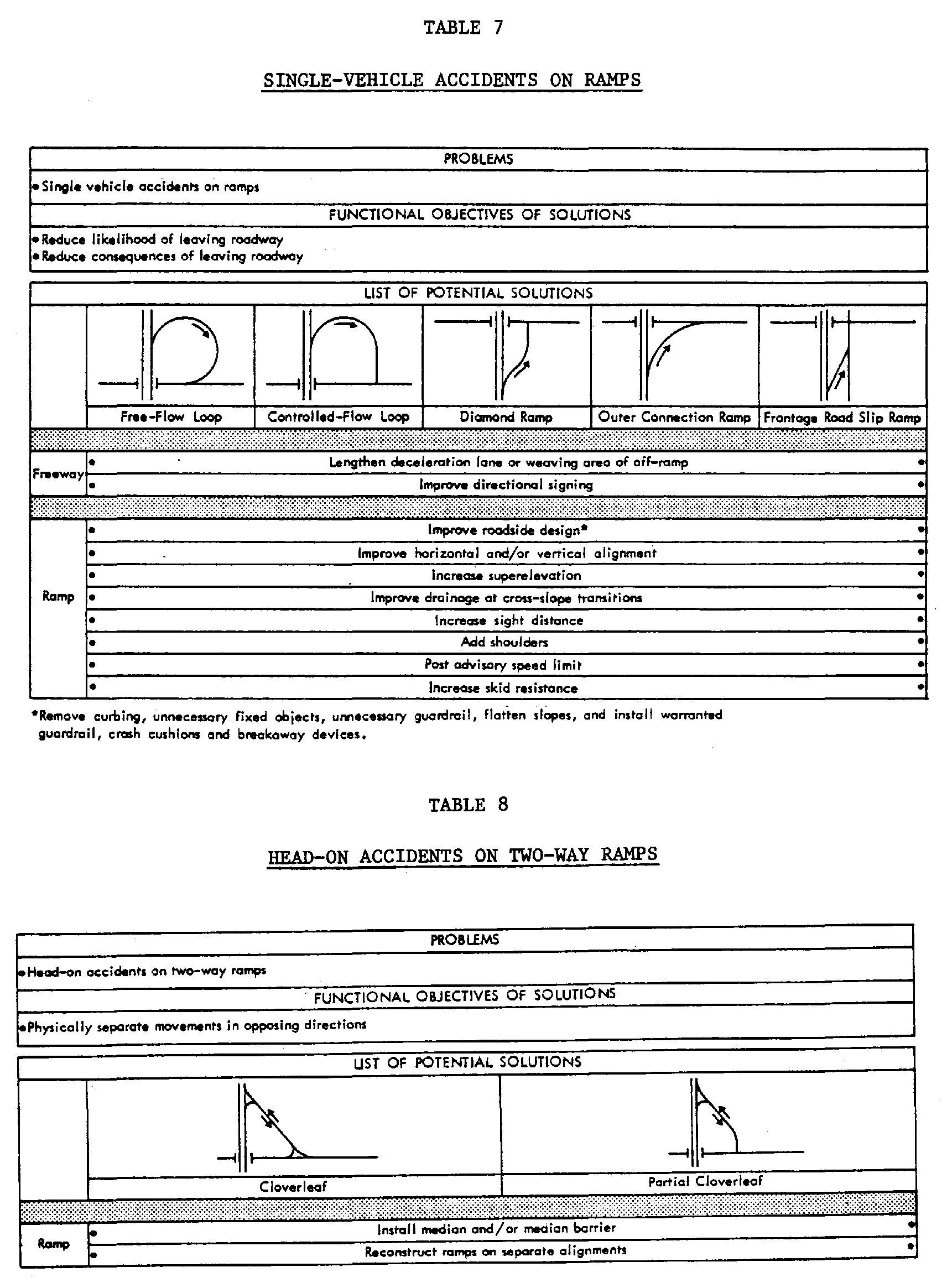


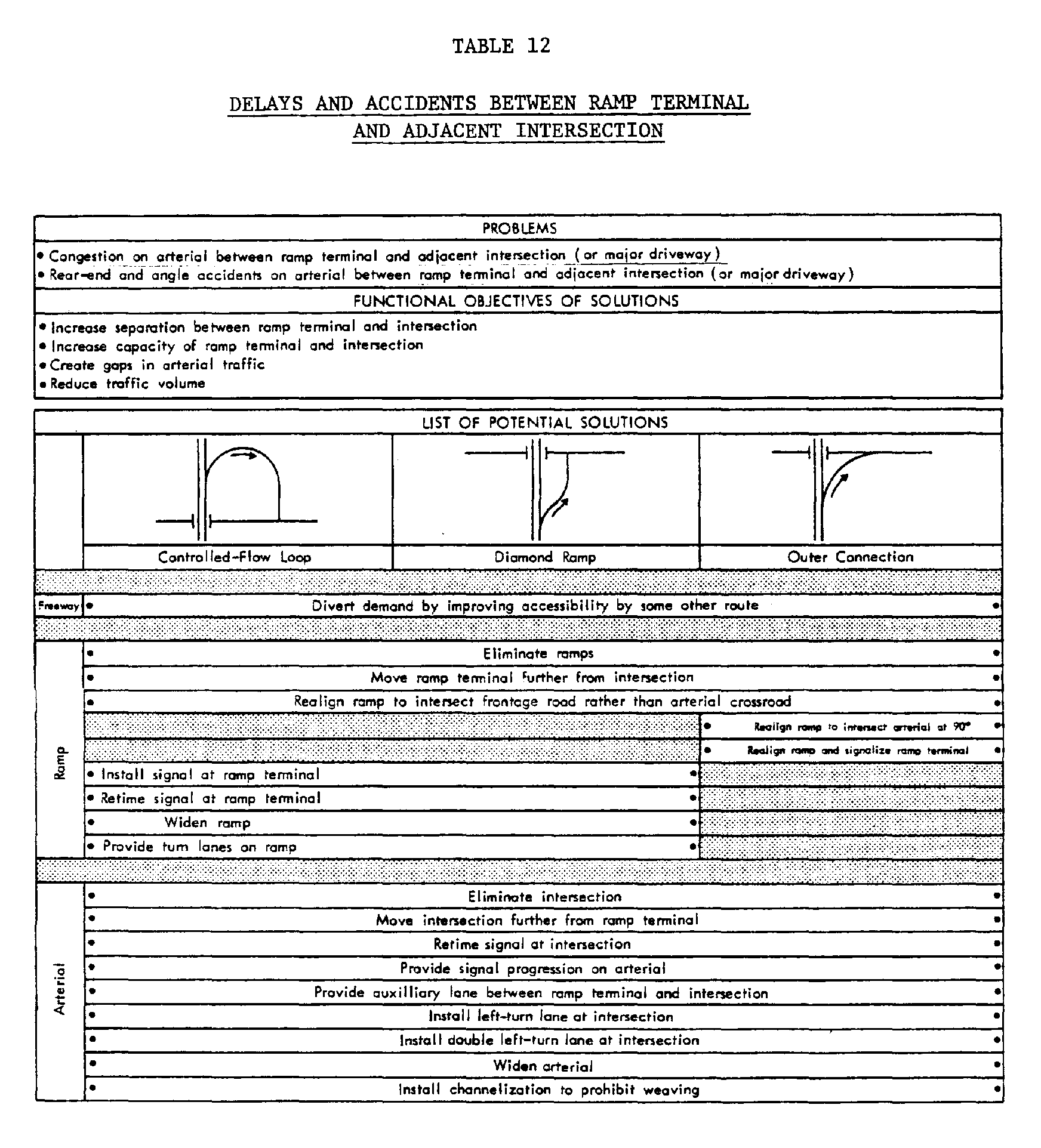
The charts can be used in the following manner. First, review all nine charts to select the one(s) appropriate for the operational or safety problems at the interchange in question. Second, select the column appropriate for the type of ramp or interchange configuration at the problem location. Third, review all solutions in the selected column. Solutions which are not physically feasible at the particular location or are not appropriate for the site-specific problem can be eliminated at this stage.
Judgement must be exercised in interpreting these charts since, for example, installation of a signal is not an appropriate countermeasure at a location that is already signalized. Rather than introducing more classifications to the charts, such as signalized vs. unsignalized ramp terminals, it is assumed that the user is capable of eliminating such inappropriate solutions very quickly.
It should be recognized that no set of charts, such as those presented in Tables 4-12, can present every solution appropriate for a particular problem and location. The scope of the charts has been limited to improvements that preserve or are closely related to the existing interchange configuration. Although major rebuilding could alleviate a problem by a complete change in the interchange configuration, this is often infeasible in urban and suburban areas due to right-of-way restrictions. In addition, some interchanges will always present unusual geometric or traffic conditions that cannot be generalized. For these reasons, the charts also identify the functional objectives of the solutions presented. These functional objectives are the basic principles that underly the solutions and these basic principles are applicable even when the specific solutions in the charts are not. Additional solutions will often be apparent if the appropriate functional objectives are kept in mind. It is recommended that—in every case—the engineer should consider whether solutions not included in the charts are physically feasible and appropriate to the problem.
In the final step, the solutions that have been identified should be used—alone or in combination with one another—to define a set of formal alternatives for consideration in the design process. Whenever possible, preference should be given to alternatives that treat the basic cause of a problem rather than merely its symptoms. For example, where traffic backs onto the mainline freeway lines from a diamond ramp, the basic problem is usually the capacity of the crossroad ramp terminal and solutions which increase its capacity are preferable to those that merely increase the vehicle storage available on the ramp.
There is a strong temptation to introduce budgetary constraints at this stage and eliminate the more costly alternatives. However, the retention of all reasonable alternatives and their analysis in more or less depth, as described in Sections VII and VIII, is recommended to ascertain the costs and relative merits of the alternatives. Even if funds are not immediately available to construct the “ultimate” improvement for the interchange, it may be possible to construct a smaller project which contributes to the “ultimate” solution through staged construction. For example, widening of a diamond off-ramp to increase vehicle storage may contribute to a later capacity improvement of the crossroad ramp terminal.
B. General Classes of Problems and Solutions
The nine charts used to identify alternative interchange improvements each address one or more related operational and safety problems that frequently occur at freeway-arterial interchanges. The nature of these nine sets of problems and their general solutions are briefly discussed in this section. The problems included in the charts illustrate the critical role of the arterial crossroad ramp terminals as the source of problems at freeway-arterial interchanges. A review of 40 interchange rehabilitation projects, presented in Volume III, found that 85 percent of the projects involved improvements to the crossroad ramp terminals and that most improvements to the arterial crossroad and the ramps were related to the ramp terminals. Consequently, the charts indicate a heavy emphasis on solutions involving the crossroad and ramps.
- Off-Ramp Delays and Rear-End Accidents: A common problem of freeway-arterial interchanges is the back up of traffic on an off-ramp resulting from insufficient capacity of the crossroad ramp terminal relative to the ramp volume. While most typical of diamond and partial cloverleaf interchanges, this problem could conceivably occur at any freeway-arterial interchange. The capacity deficiency at the crossroad ramp terminal can lead both to excessive delay for off-ramp motorists and to rear-end accidents at the end of the queue. The problem is generally considered most severe if the queue of vehicles extends into the through lanes of the mainline freeway. Table 4 presents a variety of improvements to the interchange configuration and to individual interchange elements each of which is intended to increase capacity, increase vehicle storage or reduce traffic volume. Judgment must be used in interpreting this chart because, for example, geometric improvements to the mainline freeway are appropriate only when the queue of vehicles extends beyond the off-ramp gore. As noted in the lower portion of the chart, capacity improvements to the arterial crossroad (presented in Table 6), can also contribute to the solution of these problems because such solutions can increase the capacity (green-to-cycle time ratio) for the off-ramp approach.
The countermeasures “optimize existing signal,” which appears in Table 4 and several other tables, refers to a variety of signal improvements including adjusting timing, relocation of signal heads, installation of mast arms, installation of visors, and/or black plates, etc.
- On-Ramp Delays and Accidents: An analogous problem can also occur when there is insufficient capacity for traffic entering the mainline freeway from an on-ramp. Such problems can arise from geometric constraints or from extremely heavy volumes. (The solution of problems caused by heavy freeway volumes are not addressed directly here because they are not interchange-related, but some solutions presented here could be used to accommodate, rather than solve, freeway-related problems.)
Merging accidents involving vehicles entering mainline freeway are also included here because here because many of the same countermeasures are effective. Table 5 illustrates appropriate solutions for five on-ramp configurations. These countermeasures include those that increase capacity, increase vehicle storage, reduce traffic volume, and reduce traffic conflicts. Geometric improvements to the arterial crossroad are appropriate only when the queue of off-ramp vehicles extends onto the crossroad.
- Arterial Crossroad Delays and Accidents: Table 6 addresses the solution of a variety of common interchange problems including delays for through, right-turn and left-turn vehicles on the arterial crossroad, and several types of accidents at crossroad ramp terminals including rear-end, right-turn, and left-turn accidents. For these problems, it is most convenient to classify solutions based on the overall interchange configuration rather than the configuration of an individual ramp. There are a large number of conventional traffic engineering solutions applicable to interchange configurations with at-grade ramp terminals—partial cloverleafs, diamonds, and slip-ramp diamonds. However, Table 6 illustrates graphically that there are very few solutions appropriate for the full cloverleaf configuration. In many cases, the capacity of the crossroad in the interchange area may be constrained by an adjacent intersection (such as a frontage road) as well as by the ramp terminal. Most of the solutions in Table 6 are also applicable to frontage road intersections. A common problem involving a frontage road intersection located very close to a crossroad ramp terminal is treated as a special case in Table 12.
- Single-Vehicle Accidents on Ramps: One common interchange problem that does not directly involve the crossroad ramp terminals is the single vehicle run-off-road accident. This problem is often identified by observation of erratic maneuvers or roadside damage rather than by accident records. There has been considerable effort in recent years to decrease the frequency and, especially, the severity of roadside accidents based on the principles of the AASHTO Yellow Book1 including gore area improvements, barrier installation, breakaway devices, etc. Table 7 presents ten general countermeasures to combat single vehicle run-off-road accidents. The functional objectives of these countermeasures are either to reduce the likelihood or consequences of leaving the roadway. The same set of countermeasures applies to all types of ramps.
- Head-On Accidents on Two-Way Ramps: Some older cloverleaf and partial cloverleaf interchanges have two-way ramps where the two directions of travel are separated by either a painted centerline or a very narrow median. Such locations have the potential for head-on accidents, which can be alleviated by installation of a median and/or median barrier or by reconstruction of the ramps on separate alignments, as indicated in Table 8. (This design is also susceptible to wrong-way movements onto the freeway or arterial—see Table 10.)
- Merging Accidents at Entrance to On-Ramp or Frontage Road: Merging accidents can occur at an at-grade crossroad ramp terminal or frontage road intersection as right-turn and left-turn vehicles from the crossroad come into conflict. The functional objectives of solutions for this problem involve separating the conflicting vehicles in space or in time, or reducing the traffic volumes in conflict. The solutions, given in Table 9, include addition of another ramp to divert traffic; improved channelization of the ramp terminal or frontage road intersection; widening of the on-ramp or frontage road; signalization with a protected left-turn phase; and, converting the arterial crossroad to one-way traffic.
- Wrong-Way Accidents on Ramp or Freeway: Wrong-way accidents can occur on an off-ramp or mainline freeway when arterial crossroad vehicles enter an off-ramp in the wrong direction. Countermeasures for this type of accident, given in Table 10, are intended to discourage wrong-way entries by provision of all movements at partial interchanges; realignment of off-ramp terminal channelization (islands and medians); signing improvement; installation of active warning devices; making frontage roads one-way; and moving slip ramps upstream.
- Congestion and Accidents with Mainline Freeway Weaving Areas: A predominant interchange-related problem on mainline freeways is congestion and accidents in weaving areas within full cloverleaf interchanges or between adjacent interchanges. The functional objectives for solution of these problems include elimination of the weaving area; lengthening the weaving area; separating the weaving area from the through lanes; or reducing the traffic volumes. Table 11 presents a variety of freeway, ramp, and interchange configuration-related solutions to the problems of traffic operations in weaving areas.
- Congestion and Accidents on Arterial Between Ramp Terminal and Adjacent Intersection: A common interchange-related problem occurs when a frontage road intersection (or major driveway) is located in close proximity to a ramp terminal. The operation of the ramp terminal and frontage road intersections may interfere with one another, and congestion and accidents may occur at both locations, and in between them on the arterial crossroad. Such problems occur in two distinct, but closely related situations.
The first situation can occur between the free-flow outer connection off-ramp of a full cloverleaf and a signalized frontage road intersection. In the weaving area between the ramp terminal and the signal, crossroad vehicles change lanes to the right to turn right onto the frontage road and ramp vehicles change lanes to the left to turn left onto the frontage road or go straight on the arterial crossroad. Weaving maneuvers in this area are often constrained by queues of vehicles that form when the frontage road signal is red. This situation illustrates the basic incompatibility between the free-flow nature of the ramp and the interrupted-flow nature of the signalized frontage road intersection.
The second situation occurs between a controlled-flow off-ramp terminal, such as found in a diamond or partial cloverleaf interchange,
and a frontage road intersection. The second situation differs from the first because both intersections may be signalized. However, weaving problems may still occur on the arterial crossroad between the intersections and, if the ramp-terminal has a free-flow right-turn lane, traffic operational problems identical to those described for the first situation may occur.
Table 12 illustrates several improvements to the freeway, ramp and arterial crossroad that can be employed to alleviate these problems. The functional objectives of these solutions are to increase the separation between ramp terminals and intersections; increase the intersection capacity; create gaps in arterial traffic for weaving vehicles; and reduce traffic volumes.

